N5 Net Software Repository
Your one-stop for all your software needs.
Search N5 Net Software Repository:
Search Files
Sponsor:
Browse:
- Audio & Multimedia (1643)
- Business (3971)
- Communications (1197)
- Desktop (222)
- Development (607)
- Education (291)
- Games & Entertainment (731)
- Graphic Apps (698)
- Home & Hobby (108)
- Network & Internet (593)
- Security & Privacy (536)
- Servers (69)
- System Utilities (31267)
- Web Development (297)
Areas Of Interest
Authors Area
Are you a software author? Take a look at our Author Resource Center where you will find marketing tools, software specifically created for promoting your software and a ton of other helpful resources.
Search: atomic concepts software
Education :: Mathematics
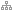
The automata which are modeled in this application are composed of a set of spheres whose size and axis are relative to one another, and where each sphere is rolling upon the surface of one other sphere in a fully deterministic pattern in space and in time. The paths through space taken by one or more points within each sphere can also be visualized as the automaton carries out is choreographed movements.
Windows | Freeware
Read More | Download Now
Education :: Mathematics
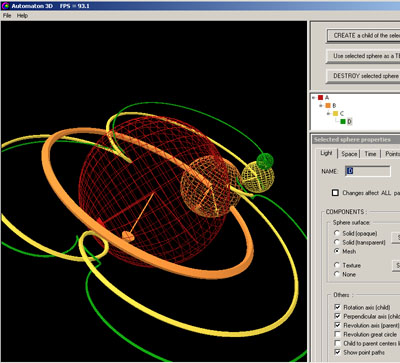
The automata which are modeled in this application are composed of a set of spheres whose size and axis are relative to one another, and where each sphere is rolling upon the surface of one other sphere in a fully deterministic pattern in space and in time. The paths through space taken by one or more points within each sphere can also be visualized as the automaton carries out is choreographed movements.
Windows | Freeware
Read More | Download Now
Education :: Mathematics
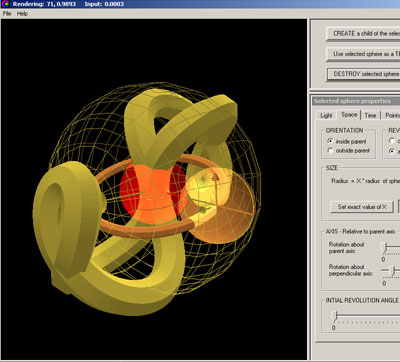
One might wonder if there is a 3-dimensional golden-rectangular-solid that is analagous to the 2-dimensional golden-rectangle, which can be sub-divided recursively so that each left-over rectangular solid has the same proportions as the original rectangular solid. The 3D analogue to the 2D golden rectangle does indeed exist, and is depicted by this application.
Windows | Freeware
Read More | Download Now
Education :: Mathematics
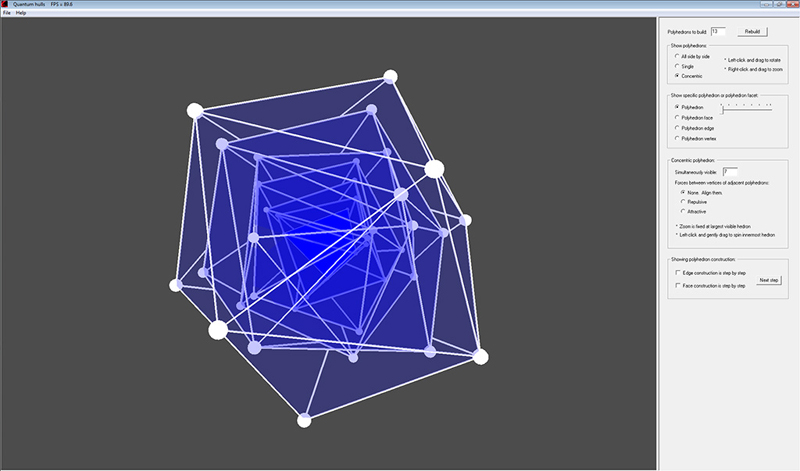Visualization of the polyhedra whose vertices have repelled each other on the surface of a sphere, until their positions have stabilized. The simplest such polyhedron has 4 vertices, and naturally becomes a tetrahedron. The remaining polyhedra, with an integral number of vertices, are NOT regular polyhedra. I call them "quantum hulls" because they are all convex hulls with triangular faces, and the number of vertices is quantized.
Windows MAC | Freeware
Read More | Download Now